Programmation logique

I. Présentation

La programmation logique est un paradigme de programmation déclaratif très différent de tout ce que vous avez pu voir jusqu'à présent. Il repose essentiellement sur la logique des prédicats (ou logique du premier ordre). Il y a peu de langages mettant en oeuvre la programmation logique. On pourra toutefois en citer 2 : Prolog et mercury. Prolog restant malgré tout la référence, c'est avec ce langage que ce cours va être illustré.

Prolog est un langage créé en 1972 (grande année !) par un français (Cocorico !) : Alain Colmerauer. C'est un langage principalement utilisé dans le domaine de l'intelligence artificielle, mais aussi dans le traitement du langage.

Pour utiliser Prolog, vous pouvez bien sûr installer swi-prolog sur votre marchine, mais le plus simple pour tester les exemples de ce cours est de vous rendre sur l'interpréteur en ligne swish.

II. Principe général de fonctionnement avec un premier exemple

Dans Prolog, un programme est en fait une base de faits et règles, et le programme est en quelque sorte exécuté en posant une question dans l'interpréteur.

Pour illustrer le fonctionnement de Prolog, nous allons partir sur la manipulation de l'arbre généralogique suivant, très conventionnel il est vrai (couples hétérosexuels, pas de remariages, etc.), mais c'est pour la bonne cause : vous simplifier la vie !) :

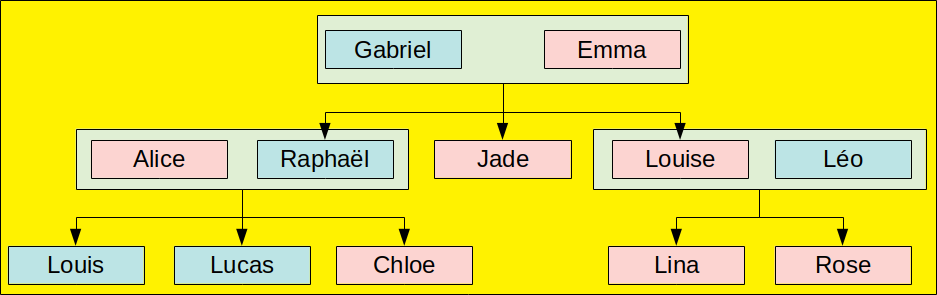
Arbre généalogique

Dans notre base de faits, nous allons représenter différents types d'information pour représenter cet arbre :

Par exemple, pour représenter le fait que Gabriel est de sexe masculin, on va tout simplement écrire :

  masculin(gabriel).

Vous pourrez noter que :

En prolog, les mots qui ne sont pas des mots du langage (comme "gabriel" ou "masculin" ici) sont appelés des atomes. Attention : ce ne sont pas des données de type "chaîne de caractères" ! (les chaînes de caractères existent en Prolog, mais n'ont pas d'intérêt si elles ne doivent pas être manipulées et si on n'est pas dans un contexte d'entrée/sortie). Ils peuvent tout à fait correspondre à des prédicats, comme "masculin" ici. Rappelons qu'un prédicat peut être vu comme une fonction renvoyant vrai ou faux.

Ici, en déclarant masculin(gabriel), je déclare que la valeur du prédicat masculin est vrai pour la valeur gabriel. Mais dans le même temps, en Prolog règne l'hypothèse du tiers exclu : cela signifie que tout ce qui n'est pas explicitement vrai est faux. Du coup, si ma base de faits et règles se limite à cette seule déclaration, cele signifie en même temps que je déclare que Emma n'est pas de sexe masculin, mais aussi que Raphaël n'est pas de sexe masculin. Vérifions tout cela avec swish.

Lorsque vous allez sur le site de swish et que vous cliquez sur "Programme", s'ouvre devant vous l'interface suivante :

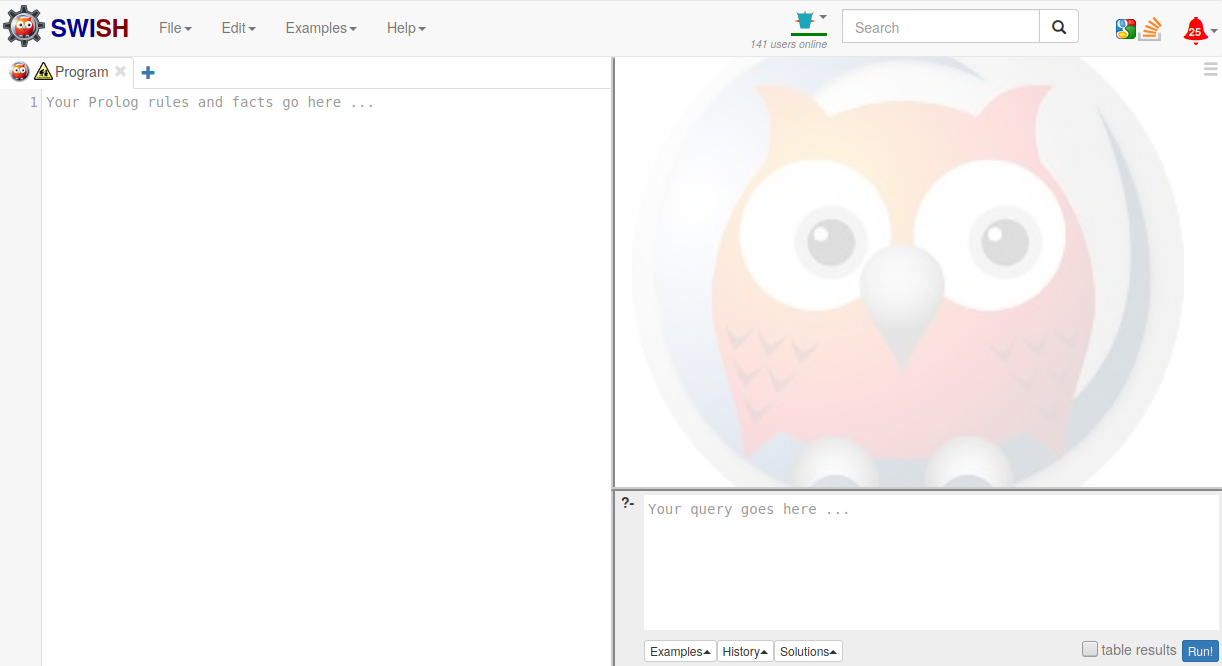
Interface de swish

Dans cette interface :

  1. La partie gauche est dédiée à la saisie de la base de faits et règles ;
  2. La partie en bas à droite est la partie dédiée à la saisie des questions ;
  3. La partie en haut à droite est destinée à l'affichage des résultats ;
  4. Le bouton Run! en bas à droite sert à poser la question saisie.

Remplissez maintenant la base de fait avec masculin(gabriel). Pour interroger la base, nous allons maintenant poser des questions dans la zone dédiée. Par exemple, pour savoir si gabriel est de sexe masculin, il est possible de saisir la question suivante : masculin(gabriel).. En cliquant sur le bouton Run!, on obtient l'affichage suivant :

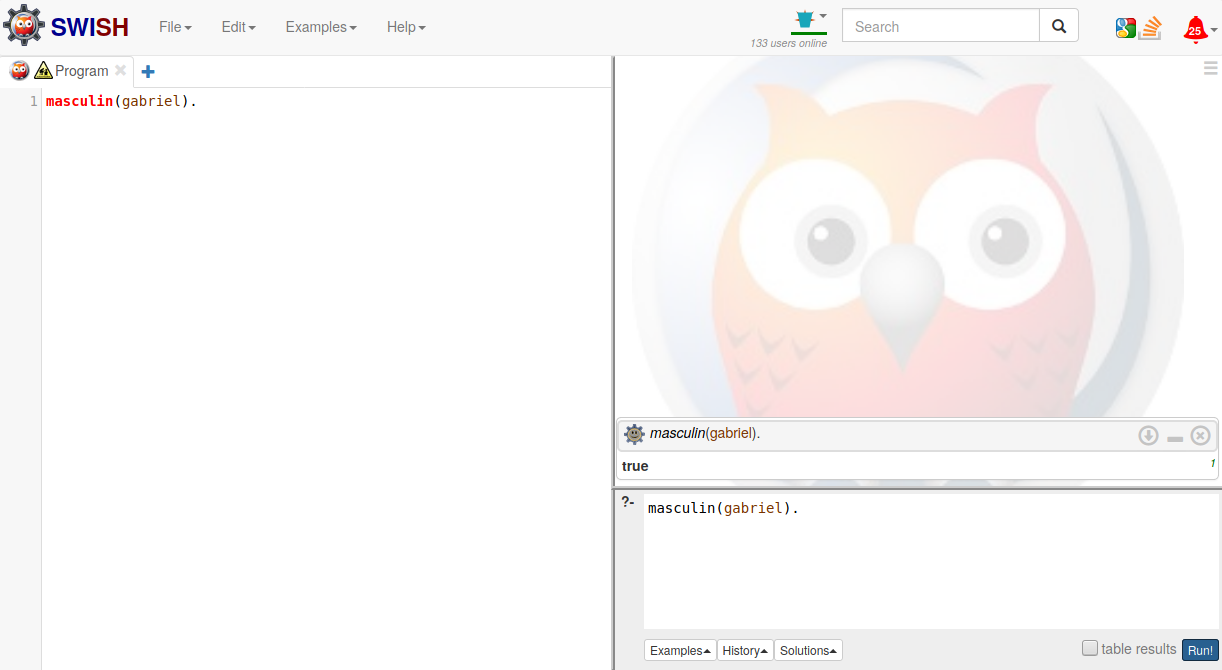
Premier exemple d'utilisation de swish

Comme on peut le voir la réponse à la question est bien évidemment True. Par ailleurs, il est important de distinguer la différence sémantique entre le masculin(gabriel). saisi à gauche, qui correspond à un fait (on sait que gabriel est de sexe masculin) et le masculin(gabriel)., qui correspond à une question (est-ce-que je peux déduire de ma base que gabriel est de sexe masculin ?).

Exercice 1 : Vérifiez que emma n'est pas de sexe masculin et que raphael n'est pas de sexe masculin non plus.

III. Notion de variable logique

En Prolog, les variables ne sont pas, comme dans les autres langages informatiques, des noms référençant des zones mémoires dont la valeur peut changer :

Une variable logique est proche de la variable en matématiques : c'est un nom représentant une valeur que je peux connaître (on dit alors que la variable est liée) ou ne pas connaître (on dit alors que la variable est libre). Une variable est représentée en Prolog par un mot commençant par une majuscule.

A. Variable utilisée dans une question

Quand une variable est utilisée dans une question, cela revient à demander à Prolog de résoudre une équation en trouvant une valeur pour la variable qui permette de satisfaire la question.

Ainsi, si l'on saisit maintenant la question suivante :

masculin(X).

Prolog trouve une valeur de X permettant de satisfaire ce prédicat et fournit la réponse : X = gabriel.

Mais que se passe-t-il s'il y a maintenant plusieurs solutions ? Étoffons en effet la base en précisant que Raphaël, Léo, Louis et Lucas sont également de sexe masculin :

masculin(gabriel).
masculin(raphael).
masculin(leo).
masculin(louis).
masculin(lucas).

Que se passe-t-il alors si l'on redemande à Prolog de trouver une valeur de X qui permettent de vérifier masculin(X) ?

Cette fois-ci, Prolog affiche le résultat suivant :

Exemple d'une solution multiple

Prolog nous propose donc une valeur pour X (gabriel), mais, via le bouton Next, il vous propose de chercher s'il n'y aurait pas une autre valeur. Chaque clic sur Next vous propose une nouvelle valeur, jusqu'à ce qu'il n'y ait plus de solution.

B. Variable utilisée dans la base de faits et règles

Lorqu'une variable est utilisée dans un fait, il faut considérer cela comme une variable quantifiée universellement. Ainsi, si l'on rajoute le fait suivant à notre base :

personne(P).

Cela revient à écrire : ∀ p.(personne(p)).

Complétez votre base de faits et règles avec de fait (en négligeant pour le moment l'aversissement Singleton variables: [P]), et testez les questions suivantes :

Exercice 2 : Complétez la base de faits et règles pour représenter le genre (masculin ou féminin) de toutes les personnes présentes dans l'arbre généalogique. Vous noterez que Prolog vous demande (pour éviter d'éventuels erreurs) de regrouper les déclarations concernant le même prédicat). 

masculin(gabriel).
masculin(raphael).
masculin(leo).
masculin(louis).
masculin(lucas).
feminin(emma).
feminin(alice).
feminin(jade).
feminin(louise).
feminin(chloe).
feminin(lina).
feminin(rose).

III. On continue

A. Prédicats ayant une arité supérieure à 1

Pour représenter que Raphaël est l'enfant d'Emma, on va rajouter un nouveau prédicat, enfant, qui sera un prédicat à 2 paramètres (on parle de prédicat d'arité 2) : l'un correspondant à l'enfant (Raphaël), l'autre correspondant au parent (Emma). On représente en général l'arité du prédicat en faisant suivre le nom du prédicat par un "/" suivi de l'arité. Ainsi, donc notre cas, on parlera des prédicats masculin/1 et enfant/2. Par convention, on met souvent en premier argument celui qui correspond à la "réponse" que suggère le nom du prédicat. On peut donc étoffer notre base de faits en rajoutant le fait suivant :

  enfant(raphael, emma).

Exercice 3 : complétez la base de faits et règles avec les prédicats enfant/2 et mari/2 pour terminer la représentation de l'arbre généalogique.

  enfant(raphael, gabriel).
  enfant(raphael, emma).
  enfant(jade, gabriel).
  enfant(jade, emma).
  enfant(louise, gabriel).
  enfant(louise, emma).
  enfant(louis, alice).
  enfant(louis, raphael).
  enfant(lucas, alice).
  enfant(lucas, raphael).
  enfant(chloe, alice).
  enfant(chloe, raphael).
  enfant(lina, louise).
  enfant(lina, leo).
  enfant(rose, louise).
  enfant(rose, leo).
  mari(gabriel, emma).
  mari(raphael, alice).
  mari(leo, louise).

B. Après les faits, les règles

Jusqu'à présent, notre base de faits et règles ne contenait que des faits, ce qui limitait beaucoup son utilisation. Nous allons maintenant lui rajouter des règles (oui, je sais, je n'ai jamais vraiment dit ce qu'était un fait ni ce qu'était une règle. Mais ça viendra...).

Nous aimerions par exemple pouvoir savoir qui est le père Raphaël. C'est clairement une information qui n'est pas présente telle qu'elle dans notre base. Mais c'est une information que nous (humains) pouvons déduire. En effet, nous savons qu'un père, c'est un parent de sexe masculin. Ou encore, pour qu'une personne P soit père d'une personne E, il faut que E soit l'enfant de P et que P soit de sexe masculin. C'est même une condition suffisante pour tout couple (P, E). En logique, on noterait cela ainsi :

 ∀(P,E).(masculin(P) ∧ enfant(E,P) → pere(P, E))
Ceci constitue une règle que nous allons pouvoir rajouter à notre base de faits et règles sous la forme suivante : 
pere(P,E):- masculin(P), enfant(E, P).

Par rapport à la notation logique, on observe quelques différentes :

On appelle également pere(P,E):-masculin(P), enfant(P,E) une clause, pere(P,E) est la tête de la clause, et masculin(P) et enfant(P,E) sont les antécédents de la clause.

Il est alors possible d'utiliser ce nouveau prédicat pere/2 de plusieurs façons différentes, en posant à Prolog les différentes questions suivantes ::

Ainsi, comme on peut le voir, un prédicat en Prolog est utilisables de plusieurs façons différentes.

Une particularité de prolog est l'existence d'un moteur d'inférence, qui traite chaque nouvelle question, et dont le fonctionnement peut être approximé ainsi :

traiter (question, affectations):
  listeClausesAvecAffectations = trouverClausesCompatibles(question, affectations)
  if listeClausesAvecAffectations == []:
    return (False, {})
  else:
      for (clause, affectations) in listeClausesAvecAffectations:
        listeAntecedents = clause.antecedents
        if listeAntecedents == []:
          yield (True, affectations)
        else:
          for antecedent in listeAntecedents:
            (resultat,affectations) = traiter(antecedent, affectations)
            if not(resultat):
              return (False, {})
          yield (True, affectations)
trouverClausesCompatibles(question, affectations):
  listeClausesAvecAffectations = []
  questionAvecAffectations = appliquerAffectation(question, affectations)
  for clause in baseFaitsEtRegles:
    tete = clause.tete
    teteAvecAffectations = appliquerAffectation(tete, affectations)
    (unificationPossible, affectationsUtilisees) = tenterUnifier(questionAvecAffectations, teteAvecAffectations)
    if unificationPossible:
      listeClausesAvecAffectations = listeClausesAvecAffectations.append(dict(**affectations, affectationsUtilisees))
  return listeClausesAvecAffectations

Si on applique cet algorithme à la résolution de la question pere(X,Y), voila ce que cela donne :

C. Et la récursivité, dans tout ça ?

Bien sûr, Prolog permet la récursivité. C'est d'ailleurs la seule façon d'itérer. Voici par exemple une façon de calculer les termes de la suite de Fibonacci (oui, "encore !", je sais...) en Prolog :

fibo(1,0).
fibo(1,1).
fibo(U, N):- N1 is N-1, N2 is N-2, fibo(U1, N1), fibo(U2, N2), U is U1 + U2.

Et pour connaître U6, il suffit de poser la question fibo(U,6).

Et si on doit gérer des collections de données ? Il y a les listes, bien sûr ! Voici par un exemple un programme (pas du tout efficace) permettant de générer la liste des termes de... la suite de Fibonacci (oui, c'est maladif, chez moi) jusqu'au n-ième :

listeFibo([], 0).
listeFibo(L, N):- N > 0, N1 is N-1, listeFibo(FN1, N1), fibo(Un, N), append(FN1, [Un], L).

D. Et la cerise sur le gâteau

Voici un petit programme qui donne toutes les solutions les plus courtes pour résoudre le problème du compte est bon : il s'agit de la partie "chiffres" du jeu Des chiffres et des lettres, où il faut réussir à obtenir un nombre (compris entre 100 et 999) à partir de 6 autres nombres, en utilisant les 4 opérations de base et en restant dans l'ensemble des naturels.

Vous n'êtes pas obligés de tout comprendre, mais si ça vous intéresse, n'hésitez pas à y jeter un oeil et à poser les questions que vous voulez. 

bonCompte(N, [N | _],[]):-!.
bonCompte(N, L,[Detail|Details]):- choisir2elements(Op1, Op2, Reste, L),
		  calcul(Resultat, Op1, Op2, Detail),
		  bonCompte(N, [Resultat|Reste],Details).

choisir2elements(Operande1, Operande2, Reste, Liste):-
    select(Operande1, Liste, Reste1),
    select(Operande2, Reste1, Reste),
    Operande1 >= Operande2.

calcul(Res, Op1, Op2, [Op1, '+', Op2, '=', Res]):- Res is Op1 + Op2.
calcul(Res, Op1, Op2, [Op1, '*', Op2, '=', Res]):- Op2 > 1, Res is Op1 * Op2.
calcul(Res, Op1, Op2, [Op1, '-', Op2, '=', Res]):- Res is Op1 - Op2, Res > 0, Res \== Op2.
calcul(Res, Op1, Op2, [Op1, '/', Op2, '=', Res]):- Op2 > 1, Res is Op1 / Op2, integer(Res), Res \== Op2.

longueurMin(Longueur, [Liste]):-!, length(Liste, Longueur).
longueurMin(Longueur, [Liste|ListeDeListes]):-!, longueurMin(L1, ListeDeListes), length(Liste, L2), min(Longueur, L1, L2).

min(X, X, Y):-X < Y, !.
min(Y, X, Y):-X >=Y, !.

gardeCourts(Reste, Liste):- longueurMin(Longueur, Liste), gardeCourts(Reste, Longueur, Liste).
gardeCourts([], _, []):-!.
gardeCourts(Reste, Longueur, [X|Xs]):- length(X, L), L > Longueur, !, gardeCourts(Reste, Longueur,  Xs).
gardeCourts([X|Reste], Longueur, [X|Xs]):- length(X, L), L =< Longueur, !,  gardeCourts(Reste, Longueur, Xs).

optimum(Compte, Plaques, Solutions):-setof(Resultats, bonCompte(Compte, Plaques, Resultats), ToutesSol), gardeCourts(Solutions, ToutesSol).

Si vous souhaitez par exemple savoir comment obtenir 749 à partire des nombres 1, 3, 5, 7, 9, 10, il suffit de poser la question suivante :

  optimum(749, [1, 3, 5, 7, 9, 10], S).

Et parmi les solutions proposées, vous aurez par exemple la solution suivante, qui vous avait bien évidemment sauté aux yeux :

   5 + 3 =   8
  10 + 1 =  11
  11 * 9 =  99
  99 + 8 = 107
 107 * 7 = 749