Piles

I. Définition

A. Définition informelle

Les piles sont des structures appelées également structures LIFO : Last In, First Out. Elle sont appelées piles car elles fonctionnent de façon similaire à une pile d'assiette : la dernière assiette rangée (sur le dessus) sera la première assiette à resservir. C'est une structure très souvent utilisée en informatique, notamment parce qu'elle est bien adaptée à la récursivité.

Outre la classique pile d'assiettes, un autre exemple de pile tiré de la vie de tous les jours se retrouve dans les instructions de montage d'un objet technique en kit : pour le démonter, il faut reprende la notice de montage de la fin vers le début.

Les piles peuvent être vues comme des listes avec un nombre restreint d'opérateurs : l'ajout au sommet ou empilement (push), la consultation du sommet (top) et le dépilement (pop).

B. Définition formelle

  Nom : Pile
  
  Constructeurs
    pileVide: Pile
    empiler: Element x Pile → Pile
  
  Opérateurs
  sommet : Pile → Element
    sommet(empiler(e,p)) = e
  
  depiler: Pile → Pile
    depiler(empiler(e,p)) = p

  estVide: Pile → Bool
    estVide(pileVide) = true
    estvide(empiler(e,p)) = false

À noter que certaines utilisations des piles requièrent d'accéder au i-ème élément à partir du sommet de la pile, mais cela sortant de la définition stricte des piles, nous ne l'aborderons pas ici.

Remarque sur l'opérateur depiler : la définition stricte classique est celle donnée ci-dessus, mais beaucoup d'implantations renvoient également l'élément dépilé.

II. Les implantations de la notion de pile

A. Le cas général

Une pile pouvant avoir a priori un nombre quelconque d'éléments, et constituant une structure linéaire, on utilise les mêmes moyens pour les implanter que ceux utilisés pour implanter des listes, à savoir des tableaux dynamiques ou des listes chaînées. Dans ce dernier cas, on utilisera des listes simplement chaînées, mais avec un chaînage sur le précédent plutôt que sur le suivant.

B. En Python

En Python, les tableaux dynamiques se prêtent très bien à l'implantation de la notion de pile, d'autant plus que les opérateurs nécessaires sont déjà fournis.

Voici maintenant comment les constructeurs et opérateurs du type Pile se retrouvent parmi les fonctionnalités des tableaux dynamiques en Python :

Constructeur /
Opérateur Équivalent Python Exemple

pileVide [] p = []

empiler append() p.append(1)

sommet [-1] s = p[-1]

depiler pop() s = p.pop()

estVide len(...) == 0 vide = len(p) == 0

Constructeur / Opérateur	Équivalent Python	Exemple
`pileVide`	`[]`	`p = []`
`empiler`	`append()`	`p.append(1)`
`sommet`	`[-1]`	`s = p[-1]`
`depiler`	`pop()`	`s = p.pop()`
`estVide`	`len(...) == 0`	`vide = len(p) == 0`

C. Ré-implanter les piles

Pour rendre plus clair la notion de pile, il est possible de ré-implanter une pile pour n'autoriser que les opérations de la structure de pile sous la forme d'une class Pile (c'est la mise en oeuvre du Pattern Façade). Cela pourrait donner la classe suivante :

class Pile:
    def __init__(self):
        self.pile = []

    def empiler(self, e):
        self.pile.append(e)

    def sommet(self):
        assert len(self.pile) > 0, "Pile vide!"
        return self.pile[-1]

    def depiler(self):
        assert len(self.pile) > 0, "Pile vide!"
        s = self.pile.pop()
        return s

    def estVide(self):
        return len(self.pile) == 0

    def __str__(self):
        retour = ""
        for e in range(len(self.pile)-1, -1,-1):
            retour += str(self.pile[e]) + '\n'
        retour += "====\n"
        return retour

Dans la suite du cours, c'est ce type Pile qui est utilisé, mais il est tout à fait possible d'utiliser directement les tableaux dynamiques

III. Quelques algorithmes utilisant les piles

A. Retourner une liste

Lorsqu'une liste ne peut être parcouru que dans l'ordre croissant des indices, la pile est bien adaptée pour retourner la liste : il suffit d'empiler un à un les éléments de la liste initiale, puis de les dépiler un à un :

def retourner(liste):
    pile = Pile()
    for element in liste:
        pile.empiler(element)
    listeInversee = []
    while not pile.estVide():
        listeInversee.append(pile.depiler())
    return listeInversee

B. Calculatrice en notation polonaise inversée

La notation polonaise inversée (ou RPN) est une écriture post-fixée des expressions arithmétiques. Dans cette notation, au lieu d'écrire l'opérateur entre les opérandes (2 + 3), on l'écrit après (2 3 +). Ainsi au lieu d'écrire :

(2 + 3) * (5 - (7 - 1))

On écrit :

2 3 + 5 7 1 - - *

Cette notation, popularisée par les calculatrics HP, présentent plusieur avantages :

Moins de caractères à taper (les parenthèses deviennent inutiles) ;
Pas de règles de priorité ;
Évaluation facile pour un programme.

L'évaluation d'une telle expression est en effet très simple : une fois l'expression découpée en unités lexicales (nombres ou opérateurs), on parcourt la liste des unités lexicales (ou lexèmes) et on procède ainsi :

Si le lexème courant est un nombre, on l'empile ;
Si le lexème courant est un opérateur :

On dépile le nombre d'opérandes requis,
On effectue le calcul,
On empile le résultat

Exercice 1 : Écrire un programme permettant d'évaluer une expression arithmétique écrite en RPN

Indication 1 : la méthode split permet facilement de découper une chaîne de caractères en unités lexicales.

Indication 1 : pour savoir si une chaîne est un nombre, on peut utiliser try: n = int(chaine) except ValueError: ...

def evaluer(expression):
    lexemes = expression.split(" ")
    pile = Pile()
    for lex in lexemes:
        operateur = False
        n = 0
        try:
            n = int(lex)
        except ValueError:
            try:
                n = float(lex)
            except ValueError:
                operateur = True
        if operateur:
            evaluerOperateur(pile, lex)
        else:
            pile.empiler(n)
    return pile.sommet()

def evaluerOperateur(pile, lex):
    if lex == '+':
        op2 = pile.depiler()
        op1 = pile.depiler()
        res = op1 + op2
        pile.empiler(res)
    elif lex == '-':
        op2 = pile.depiler()
        op1 = pile.depiler()
        res = op1 - op2
        pile.empiler(res)
    elif lex == '*':
        op2 = pile.depiler()
        op1 = pile.depiler()
        res = op1 * op2
        pile.empiler(res)
    elif lex == '/':
        op2 = pile.depiler()
        op1 = pile.depiler()
        res = op1 / op2
        pile.empiler(res)

N.B. : ici, on s'est contenté des 4 opérations de base, qui prennent toutes 2 arguments, mais on aurait très bien pu rajouter l'opérateur sqrt pour la racine carrée par exemple ; cet opérateur ne prenant qu'un argument, il ne faudrait alors appeler qu'une seule fois la méthode depiler

Exercice 1bis : Étendez votre travail pour rajouter les fonctions trigonométriques, logarithmiques, exponentielles, le nombre π, etc.

C. Pile et récursivité

Dans un programme devant explorer un espace des possibles récursivement jusqu'à trouver une solution, une pile est une structure idéale pour mémoriser le parcours réalisé jusque-là, et permettre de revenir en arrière pour explorer une nouvelle voie si nécessaire :

Explorer une voie se traduit par l'empilement de cette nouvelle voie ;
Revenir en arrière se traduit par le dépilement de la dernière voie explorer

Prenons par exemple le cas d'un robot situé sur le case e (entrée) du labyrinthe ci-dessous et cherchant à atteindre la case s (sortie), en indiquant le chemin qu'il a suivi. Le robot va procéder méthodiquement, en examinant à partir de chaque case, les 4 directions dans l'ordre Nord, Est, Sud, Ouest, en évitant de passer sur une case où il est déjà passé :

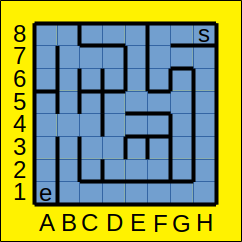
Image d'un labyrinthe

Le robot va donc explorer les cases, en effaçant sa dernière action lorsqu'il revient en arrière. Il va donc mémoriser le trajet qu'il fait en procédant ainsi :

[A1] ; on va au nord
[A1, A2] ; on va au nord
[A1, A2, A3] ; on va au nord
[A1, A2, A3, A4] ; on va au nord
[A1, A2, A3, A4, A5] ; nord, et est sont bloqués, on est déjà passé par la case au sud, et ouest est bloqué, donc on revient en arrière
[A1, A2, A3, A4] ; on va à l'est (on a déjà essayé le nord)
[A1, A2, A3, A4, B4] ; on va au nord
[A1, A2, A3, A4, B4, B5] ; on va au nord
[A1, A2, A3, A4, B4, B5, B6] ; on va au nord
[A1, A2, A3, A4, B4, B5, B6, B7] ; on va au nord
[A1, A2, A3, A4, B4, B5, B6, B7, B8] ; nord et est sont bloqués, on est déjà passé au sud, donc on va à l'ouest
[A1, A2, A3, A4, B4, B5, B6, B7, B8, A8] ; nord est bloqué, on est déjà passé à l'est, donc on va au sud
[A1, A2, A3, A4, B4, B5, B6, B7, B8, A8, A7] ; on est déjà passé au nord, est est bloqué, donc on va au sud
[A1, A2, A3, A4, B4, B5, B6, B7, B8, A8, A7, A6] ; on est déjà passé au nord, est, sud et ouest sont bloqués, donc on revient en arrière
[A1, A2, A3, A4, B4, B5, B6, B7, B8, A8, A7] ; on a déjà tenté nord, est et sud; ouest est bloqué, donc on revient en arrière
[A1, A2, A3, A4, B4, B5, B6, B7, B8, A8] ; on a déjà tenté nord, est et sud; ouest est bloqué, donc on revient en arrière
[A1, A2, A3, A4, B4, B5, B6, B7, B8] ; on a déjà tenté nord, est et sud et ouest, donc on revient en arrière
[A1, A2, A3, A4, B4, B5, B6, B7] ; on a déjà tenté nord, donc on va à l'est
[A1, A2, A3, A4, B4, B5, B6, B7, C7]
...

On peut représenter cette succession d'étapes ainsi :

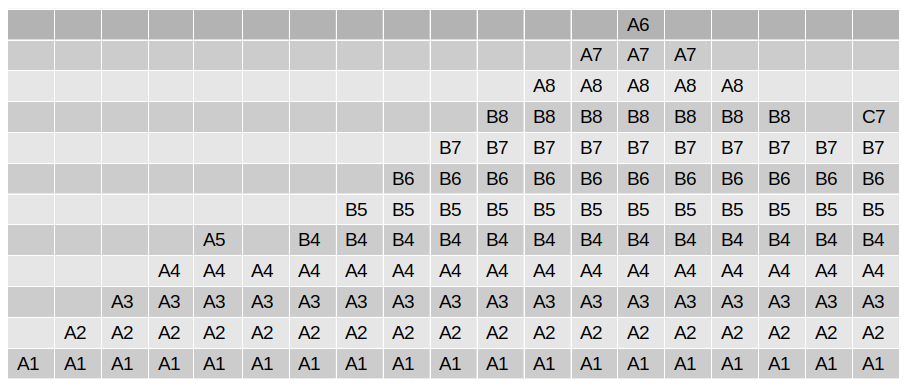
Image d'un labyrinthe

Comme on peut le voir, la pile est une structure idéale pour mémoriser le parcours en cours, puisque les opérations que l'on fait sont soit des ajouts au sommet, soit des dépilements.

Remarque : vous pourrez éventuellement revoir ce problème lorsque la partie sur les graphes sera abordée, puisqu'un labyrinthe est un cas particulier de graphe.

Exercice 2 Écrire un programme calculant un chemin solution pour le labyrinthe présenté ci-dessus.

Dans cette partie, nous construisons une représentation du labyrinthe.

colonnes = ["A", "B", "C", "D", "E", "F", "G", "H"]

barrieres = [[(1, 0, 0, 0), (1, 1, 0, 0), (0, 1, 0, 1), (0, 1, 0, 1), (0, 1, 0, 1), (0, 1, 0, 1), (0, 1, 0, 1), (1, 0, 0, 1)],
             [(1, 0, 1, 0), (1, 0, 1, 0), (1, 0, 0, 0), (1, 1, 0, 0), (1, 1, 0, 1), (1, 0, 0, 1), (1, 0, 0, 0), (1, 0, 1, 0)],
             [(1, 0, 1, 0), (1, 0, 1, 0), (1, 1, 1, 0), (1, 0, 1, 1), (0, 0, 1, 0), (0, 0, 1, 0), (1, 0, 1, 0), (1, 0, 1, 0)],
             [(1, 1, 1, 0), (1, 1, 1, 1), (1, 0, 1, 1), (1, 1, 1, 0), (0, 1, 0, 1), (0, 0, 0, 1), (1, 0, 1, 0), (1, 0, 1, 0)],
             [(0, 0, 1, 0), (1, 0, 1, 0), (0, 0, 1, 0), (0, 1, 1, 0), (1, 1, 0, 1), (0, 1, 0, 1), (1, 0, 1, 1), (1, 0, 1, 0)],
             [(1, 0, 0, 0), (1, 0, 1, 0), (1, 0, 0, 0), (1, 0, 0, 0), (1, 0, 1, 0), (1, 0, 0, 0), (0, 0, 1, 0), (1, 0, 1, 0)],
             [(1, 0, 1, 0), (1, 1, 1, 0), (0, 1, 1, 1), (0, 0, 1, 1), (1, 0, 1, 0), (1, 1, 1, 0), (0, 1, 0, 1), (0, 0, 1, 1)],
             [(0, 1, 1, 0), (0, 0, 1, 1), (0, 1, 0, 0), (0, 1, 0, 1), (0, 0, 1, 1), (0, 1, 1, 0), (0, 1, 0, 1), (0, 0, 0, 1)]]

#Construction du labyrinthe à partir des barrières déclarées dans le tableau ci-dessus.
#Structure d'une case : (nom, ouvertNord, ouvertEst, ouvertSud, ouvertOuest, visitee)
#    la première coordonnée du tuple contient le nom de la case ("A1" par exemple)
#    pour les directions, un '1' signifie que le passage est possible, un '0' qu'il y a un mur
#    la coordonnée visitée vaut 'True' si on y est déjà passée, 'False' sinon
numLigne = 1
labyrinthe = []
for ligne in barrieres:
    ligneEtiquetee = []
    numColonne = 0
    for case in ligne:
        caseEtiquetee = ((colonnes[numColonne])+str(numLigne),) + case + (False,)
        ligneEtiquetee.append(caseEtiquetee)
        numColonne += 1
    labyrinthe.append(ligneEtiquetee)
    numLigne += 1

Voici maintenant l'implantation d'un algorithme résolvant le problème du labyrinthe.

# les directions sont définies par :
#    - l'indice dans le tableau des cases,
#    - le delta en ordonnée
#    - le delta en abscisse
# exemple : pour trouver les coordonnées en allant vers le nord à partir de la case courante,
#           il faut ajoute 1 en ordonnée et 0 en abscisse.
directions = {'Nord': (1, 1, 0), 'Est': (2, 0, 1), 'Sud': (3, -1, 0), 'Ouest': (4, 0, -1)}
indicePosition = 0
indiceDeltaY = 1
indiceDeltaX = 2

# fonction récursive de recherche d'une solution
# départ : la case ou l'on est actuellement (sous la forme d'un couple (y,x)
# arrivée : la case où l'on souhaite se rendre
# pile : la pile des noms des cases par lesquelles on est passé pour atteindre la case actuelle
def trouverChemin(depart, arrivee, pile):
    if depart == arrivee:
        return (True, pile)
    # on explore toute les directions
    for direction,infoDirection  in directions.items():
        # on ne poursuit que si c'est ouvert
        if labyrinthe[depart[0]][depart[1]][infoDirection[indicePosition]] == 1:
            nouvelleCase = suivante(depart, infoDirection)
            descriptionNouvelleCase = labyrinthe[nouvelleCase[0]][nouvelleCase[1]]
            # on vérifie qu'on n'est pas déjà passé par là
            if descriptionNouvelleCase[5] == False:
                descriptionNouvelleCase = descriptionNouvelleCase[:5] + (True,)
                labyrinthe[nouvelleCase[0]][nouvelleCase[1]] = descriptionNouvelleCase
                pile.empiler(descriptionNouvelleCase[0])
                trouve, pile = trouverChemin(nouvelleCase, arrivee, pile)
                if trouve:
                    return (True, pile)
                else:
                    pile.depiler()
    return (False, pile)
        
def suivante(case, infoDirection):
    nouvelleCase = (case[0]+ infoDirection[indiceDeltaY], case[1] + infoDirection[indiceDeltaX])
    return nouvelleCase

print("============================================")
#initialisation
pile = Pile()
pile.empiler("A1")
labyrinthe[0][0] = labyrinthe[0][0][:5] + (True,)
print(labyrinthe)
print("============================================")
#recherche du chemin
res = trouverChemin((0,0), (7, 7), pile)
print(res[1])
print("============================================")